انواع دنباله ها (تصاعد)
انواع دنباله ها (تصاعد)
همانطور که میدانیم اصطلاح "سری" را برای کمیتهایی که با ضابطه معینی مرتب شدهاند بکار میبریم. هر یک از این کمیتها را یک جمله سری و جمله nام را که برحسب n نوشته میشود جمله عمومی مینامیم.
تعریف
اگر جمله عمومی یک سری بصورت  باشد که در آن d , a عددهای ثابت و مستقل از n هستند، سری را تصاعد حسابی مینامیم. از تعریف
باشد که در آن d , a عددهای ثابت و مستقل از n هستند، سری را تصاعد حسابی مینامیم. از تعریف  بدست میآید:
بدست میآید: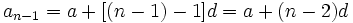
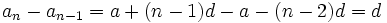
پس
تفاضل هر دو جمله متوالی تصاعد حسابی مقدار ثابت d است. به همین سبب d را
تفاضل مشترک تصاعد حسابی مینامند. همچنین به ازای n=1 ،  . پس ، a جمله اول تصاعد حسابی است. بنابراین جملههای دیگر تصاعد حسابی با افزودن مقدار ثابت d به جمله پیش از آن بدست میآید.
. پس ، a جمله اول تصاعد حسابی است. بنابراین جملههای دیگر تصاعد حسابی با افزودن مقدار ثابت d به جمله پیش از آن بدست میآید.
بقیه در ادامه
مجموع n جمله اول تصاعد حسابی
فرض میکنیم که 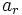 جمله rام تصاعد حسابی باشد، یعنی
جمله rام تصاعد حسابی باشد، یعنی 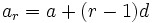 . می خواهیم
. می خواهیم 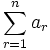 را که با
را که با  نشان داده میشود، حساب کنیم. اکنون ، سری دیگری میسازیم که در آن n جمله
اول تصاعد حسابی با ترتیب عکس قرار گرفته باشند سری جدید بصورت زیر است:
نشان داده میشود، حساب کنیم. اکنون ، سری دیگری میسازیم که در آن n جمله
اول تصاعد حسابی با ترتیب عکس قرار گرفته باشند سری جدید بصورت زیر است: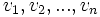
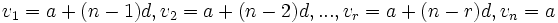
مجموع این سری همان مجموع n جمله اول تصاعد حسابی است. پس ، 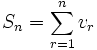
معمولا جمله nام ، یعنی 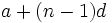 را با l نشان میدهیم. پس
را با l نشان میدهیم. پس 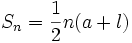
ویژگیها
- اگر عددی را به همه جملههای یک تصاعد حسابی اضافه کنیم یا از آنها کم کنیم یک تصاعد حسابی دیگر با همان تفاضل مشترک بدست میآید.
- اگر همه جملههای یک تصاعد حسابی در عددی ضرب یا بر عددی تقسیم شوند یک تصاعد حسابی دیگر با تفاضل مشترک متفاوت بدست میآیند.
برای اثبات این ویژگیها ، جمله nام تصاعد حسابی اولیه را  و جمله nام سری حاصل از اضافه کردن b به هر جمله را با
و جمله nام سری حاصل از اضافه کردن b به هر جمله را با 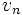 و جمله nام سری حاصل از ضرب هر جمله در k را با
و جمله nام سری حاصل از ضرب هر جمله در k را با 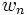 نشان میدهیم. بنابراین با تشکیل
نشان میدهیم. بنابراین با تشکیل 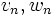 داریم: سری
داریم: سری 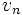 یک تصاعدحسابی با جمله اول a+b و تفاضل مشترک d است همچنین
یک تصاعدحسابی با جمله اول a+b و تفاضل مشترک d است همچنین 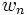 یک تصاعد حسابی با جمله اول
یک تصاعد حسابی با جمله اول 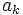 و تفاضل مشترک
و تفاضل مشترک 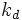 است.
است.
-
جمله nام هر تصاعد حسابی را میتوان به شکل
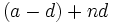 نوشت. چون a-d و d مقدارهای ثابتاند. جمله nام را میتوان به شکل A+nB
نوشت که عبارتی خطی از n است. برعکس ، اگر جمله nام یک سری عبارتی خطی از n
باشد. آن سری یک تصاعد حسابی است زیرا اگر
نوشت. چون a-d و d مقدارهای ثابتاند. جمله nام را میتوان به شکل A+nB
نوشت که عبارتی خطی از n است. برعکس ، اگر جمله nام یک سری عبارتی خطی از n
باشد. آن سری یک تصاعد حسابی است زیرا اگر 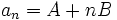 جمله nام یک سری باشد داریم:
جمله nام یک سری باشد داریم: 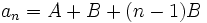 . پس این سری یک تصاعد حسابی با جمله اول A+B و تفاضل مشترک B است.
. پس این سری یک تصاعد حسابی با جمله اول A+B و تفاضل مشترک B است. -
مجموع n جمله اول یک تصاعد حسابی ، یعنی
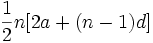 را میتوان به شکل
را میتوان به شکل 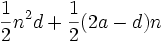 نوشت. که عبارتی درجه دوم از n است. پس مجموع n جمله اول هر تصاعد حسابی را میتوان بشکل
نوشت. که عبارتی درجه دوم از n است. پس مجموع n جمله اول هر تصاعد حسابی را میتوان بشکل 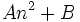 نوشت که B , A عددهای ثابت و مستقل از n هستند. برعکس ، اگر مجموع n جمله اول یک سری به شکل
نوشت که B , A عددهای ثابت و مستقل از n هستند. برعکس ، اگر مجموع n جمله اول یک سری به شکل 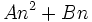 یعنی عبارتی درجه دوم از n بدون جمله ثابت باشد، آن سری یک تصاعد حسابی است.
یعنی عبارتی درجه دوم از n بدون جمله ثابت باشد، آن سری یک تصاعد حسابی است.
مقدارهای منفی n
ممکن است جملههای یک تصاعد حسابی از سوی دیگر نیز ادامه داشته باشد و جملههای 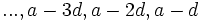 قبل از a قرار گیرند یعنی تصاعد حسابی بصورت زیر است:
قبل از a قرار گیرند یعنی تصاعد حسابی بصورت زیر است: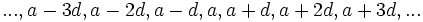
جملههای سمت چپ a با قرار دادن مقدارهای 0 و 1- و 2- و ... بجای n در 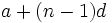 بدست آمدهاند برای بدست آوردن عده جملههایی که مجموع آنها برابر مقدار معلوم S است باید معادله
بدست آمدهاند برای بدست آوردن عده جملههایی که مجموع آنها برابر مقدار معلوم S است باید معادله 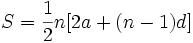 را حل کنیم. این معادله برحسب n از درجه دوم است و ممکن است یک یا هر دو ریشه آن منفی باشد. اگر
را حل کنیم. این معادله برحسب n از درجه دوم است و ممکن است یک یا هر دو ریشه آن منفی باشد. اگر 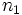 مقداری منفی از کمیت n باشد که در این معادله صدق کند داریم:
مقداری منفی از کمیت n باشد که در این معادله صدق کند داریم: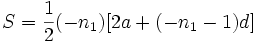
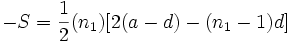
یعنی اگر از حل معادله مقداری صحیح ولی منفی برای n بدست آوریم و 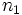 جمله قبل از a را ، که با a-d شروع میشوند در نظر گیریم مجموع -S را بدست میآوریم.
جمله قبل از a را ، که با a-d شروع میشوند در نظر گیریم مجموع -S را بدست میآوریم.
واسطه حسابی
تعریف
واسطه حسابی n کمیت برابر است با مجموع همه آنها بخشبر n. بنابراین اگر 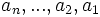 کمیتهای مورد نظر باشند واسطه حسابی آنها برابر است با
کمیتهای مورد نظر باشند واسطه حسابی آنها برابر است با 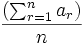 . واسطه حسابی دو کمیت b , a که آنها را c مینامیم،
. واسطه حسابی دو کمیت b , a که آنها را c مینامیم، 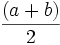 است. بنابراین ، a و c و b یک تصاعد حسابی تشکیل میدهند زیرا اگر
است. بنابراین ، a و c و b یک تصاعد حسابی تشکیل میدهند زیرا اگر 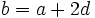 داریم:
داریم: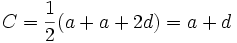
همیشه
میتوانیم بین هر دو کمیت b , a هر عده کمیت دیگر بگنجانیم بطوری که سری
بدست آمده تصاعد حسابی باشد. جملههایی را که به این ترتیب بین b , a
گنجانده میشوند واسطههای حسابی مینامیم. اگر n جمله بین b , a بگنجانیم
یک سری با n+2 جمله بدست میآید که جمله اول آن a و جمله آخرش b است.
بنابراین 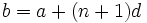 . یعنی
. یعنی 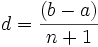 در نتیجه تصاعدهای حسابی بدست آمده چنین است:
در نتیجه تصاعدهای حسابی بدست آمده چنین است: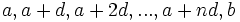
تصاعد هندسی
به دنبالهای که رابطه بازگشتی آن 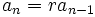 باشد یک دنباله هندسی یا تصاعد هندسی گفته میشود.
باشد یک دنباله هندسی یا تصاعد هندسی گفته میشود. 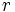 را قدرنسبت تصاعد هندسی مینامیم.
را قدرنسبت تصاعد هندسی مینامیم.
اگر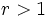 و
و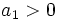 باشد، دنباله اکیداً صعودی خواهد بود و اگر
باشد، دنباله اکیداً صعودی خواهد بود و اگر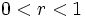 و
و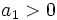 دنباله اکیداً نزولی خواهد بود.
دنباله اکیداً نزولی خواهد بود.
رابطه صریح دنباله هم به صورت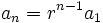 میباشد که واضح نیز به نظر میرسد.
میباشد که واضح نیز به نظر میرسد.
مسألهای که در تصاعد هندسی قابل تأمل میباشد مجموع جملات آن است.
اگر  را مجموع جملات
را مجموع جملات 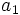 تا
تا  تعریف کنیم:
تعریف کنیم: 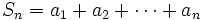
آنگاه  دنبالهای با رابطه بازگشتی زیر خواهد بود:
دنبالهای با رابطه بازگشتی زیر خواهد بود: 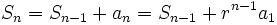
اما مقدار صریح  نیز به سادگی قابل محاسبه میباشد که داریم:
نیز به سادگی قابل محاسبه میباشد که داریم: 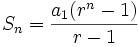
مثال
اگر  مجموع جملات دنباله هندسی با عنصر اول
مجموع جملات دنباله هندسی با عنصر اول 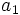 و قدرنسبت
و قدرنسبت 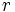 و
و 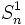 مجموع جملات دنباله هندسی دیگری با همان عنصر اول ولی قدرنسبت
مجموع جملات دنباله هندسی دیگری با همان عنصر اول ولی قدرنسبت 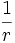 باشد. رابطه
باشد. رابطه  و
و 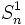 را بدست آورید؟
را بدست آورید؟
حل . 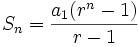
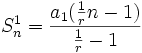
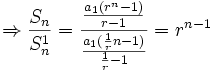
به نقل از سایت بیست ریاضی (پرشین بلاگ)


 واحد های اندازه گیری زاویه
واحد های اندازه گیری زاویه